After printing a sierpinsky triangle on Theo’s makerbot, I thought it might interest some of you to see how I generated the geometry in blender.
However, before starting I should warn you that my knowledge of Blender is virtually non-existent. The blender specific code used here to generate faces is probably not ideal and you’re very welcome to improve that part.
So, what do we want to do? Make triangles, lots of them. We probably need a function to generate triangles. Let’s stay simple and assume that a triangle is composed of 3 points. We are in a 3d space so each point will have 3 components. We shall refer to these points as Vertices. There are many ways to represent this type of data in Python. For something different, let’s try namedtuples. They provide an elegant extension to the base tuple type. They work as follows:
from collections import namedtuple
Vertex = namedtuple('Vertex', 'x, y, z') # define vertex 'type'
v1 = Vertex(0.0, 0.0, 0.0) # define a Vertex tuple, with positional arguments
v2 = Vertex(x=0.0, y=0.0, z=0.0) #define a Vertex with named arguments
x, y, z = v2 # unpack as regular tupple
x = v.x # accessible with named parameter
We can now define our triangle function
#import blender bindings
import Blender
from Blender import NMesh
from Blender.BGL import *
from Blender.Draw import *
def triangle(a, b, c):
"""generate triangle geometry
we expect a b c to be namedtuples of type Vertex"""
######### Creates a new mesh
poly = NMesh.GetRaw()
### fill vertices
v = NMesh.Vert(a.x, a.y, a.z)
poly.verts.append(v)
v = NMesh.Vert(b.x, b.y, b.z)
poly.verts.append(v)
v = NMesh.Vert(c.x, c.y, c.z)
poly.verts.append(v)
## create a face
f = NMesh.Face()
f.v.append(poly.verts[0])
f.v.append(poly.verts[1])
f.v.append(poly.verts[2])
poly.faces.append(f)
######### Creates a new Object with the new Mesh
polyObj = NMesh.PutRaw(poly)
Blender.Redraw()
My poor knowledge of blender doesn’t allow me to say much about this code. We basically use the api to generate a three point polygon. As said, please improve or correct this part.
Time for a first test!
#define the three vertices of a triangle a = Vertex(0.0, 0.0, 0.0) b = Vertex(25.0, 50.0, 0.0) c = Vertex(50.0, 0.0, 0.0) triangle(a, b, c)
We define three vertices for our test triangle and call the triangle function. The next step is to load the code in Blender’s text editor and to press Alt-p to run the code.
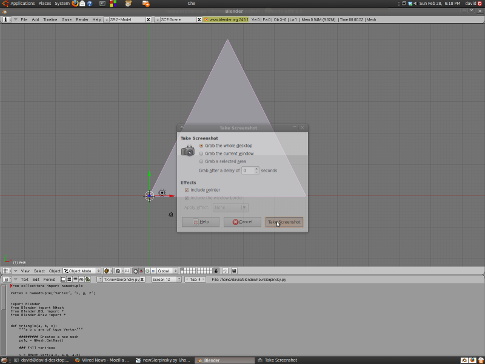
Ok, so let’s get to the meat of the problem, i.e. the recursive subdivision. I use the basic algorithm from here, and adapted it to python:
def divideTriangle(a, b, c, step):
""" recursive divide until step == 0"""
if step > 0:
#compute midpoints of sides
midpointof = lambda v1, v2: Vertex(x = (v1.x + v2.x) * 0.5,
y = (v1.y + v2.y) * 0.5,
z = (v1.z + v2.z) * 0.5)
ab = midpointof(a, b)
ac = midpointof(a, c)
bc = midpointof(b, c)
# divide all but center triangle
divideTriangle(a, ab, ac, step - 1)
divideTriangle(c, ac, bc, step - 1)
divideTriangle(b, bc, ab, step - 1)
else:
#stop recursion and generate geometry
triangle(a, b, c)
I tried to be as expressive as possible, but I have the feeling that there is something fishy in the midpoint lambda. I guess it could be simplified. But it will do for now. Let’s put it all together, and see what we get in blender.
from collections import namedtuple
import Blender
from Blender import NMesh
from Blender.BGL import *
from Blender.Draw import *
Vertex = namedtuple('Vertex', 'x, y, z')
def triangle(a, b, c):
"""a b c are of type Vertex"""
######### Creates a new mesh
poly = NMesh.GetRaw()
### fill vertices
v = NMesh.Vert(a.x, a.y, a.z)
poly.verts.append(v)
v = NMesh.Vert(b.x, b.y, b.z)
poly.verts.append(v)
v = NMesh.Vert(c.x, c.y, c.z)
poly.verts.append(v)
## create a face
f = NMesh.Face()
f.v.append(poly.verts[0])
f.v.append(poly.verts[1])
f.v.append(poly.verts[2])
poly.faces.append(f)
######### Creates a new Object with the new Mesh
polyObj = NMesh.PutRaw(poly)
Blender.Redraw()
def divideTriangle(a, b, c, step):
""" recursive divide until step == 0"""
if step > 0:
#compute midpoints of sides
midpointof = lambda v1, v2: Vertex(x = (v1.x + v2.x) * 0.5,
y = (v1.y + v2.y) * 0.5,
z = (v1.z + v2.z) * 0.5)
ab = midpointof(a, b)
ac = midpointof(a, c)
bc = midpointof(b, c)
# divide all but center triangle
divideTriangle(a, ab, ac, step - 1)
divideTriangle(c, ac, bc, step - 1)
divideTriangle(b, bc, ab, step - 1)
else:
triangle(a, b, c)
#main
a = Vertex(0.0, 0.0, 0.0)
b = Vertex(25.0, 50.0, 0.0)
c = Vertex(50.0, 0.0, 0.0)
divideTriangle(a, b, c, 5)
and in blender:
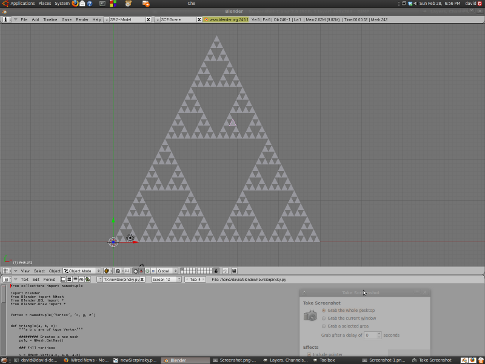
All done : )
I leave the extruded version as an exercise for the reader.
